deletion in heaps

Deleting the root node in a heap is the standard deletion operation on heap .so if it is a Max Heap we will delete the maximum element and if it is a Min heap, it will delete the minimum element.

steps:

• first replace the root (element to be deleted) by the last element.
• and now delete the last element from the Heap.
• heapify the last node placed at the position of root. because ,the last element placed in the root node may not follow the heap property. 

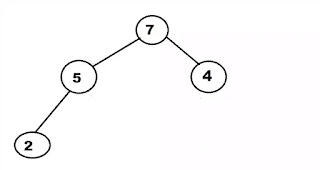
Suppose the Heap is a Max-Heap as:

The element to be deleted is root, i.e. 12.

Process:

The last element is 2.

Step 1: Replace the last element with root, and delete the previous root element .

Step 2: Heapify root.

Final Heap:

now this above figure follows the max heap properties.

Implementation:

in c++:

void heapify(int arr[], int n, int i)
{
    int largest = i; // Initialize largest as root
    int l = 2 * i + 1; // left = 2*i + 1
    int r = 2 * i + 2; // right = 2*i + 2

    // If left child is larger than root
    if (l < n && arr[l] > arr[largest])
        largest = l;

    // If right child is larger than largest so far
    if (r < n && arr[r] > arr[largest])
        largest = r;

    // If largest is not root
    if (largest != i) {
        swap(arr[i], arr[largest]);

        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}

// Function to delete the root from Heap
void deleteRoot(int arr[], int& n)
{
    // Get the last element
    int lastElement = arr[n - 1];

    // Replace root with first element
    arr[0] = lastElement;

    // Decrease size of heap by 1
    n = n - 1;

    // heapify the root node
    heapify(arr, n, 0);
}

java:

    // To heapify a subtree rooted with node i which is
    // an index in arr[].Nn is size of heap
    static void heapify(int arr[], int n, int i)
    {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2

        // If left child is larger than root
        if (l < n && arr[l] > arr[largest])
            largest = l;

        // If right child is larger than largest so far
        if (r < n && arr[r] > arr[largest])
            largest = r;

        // If largest is not root
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;

            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
        }
    }

    // Function to delete the root from Heap
    static int deleteRoot(int arr[], int n)
    {
        // Get the last element
        int lastElement = arr[n - 1];

        // Replace root with first element
        arr[0] = lastElement;

        // Decrease size of heap by 1
        n = n - 1;

        // heapify the root node
        heapify(arr, n, 0);

        // return new size of Heap
        return n;
    }

  

in the above example and code we have deleted root node for max heap

we can similarly do this for min heap 

for min heapify code visit this link:  https://www.codemummy.com/2020/10/insertion-in-heaps.html