maximum area of histogram-stack

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
                                      

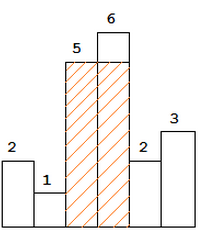
histogram where width of each bar is 1, given height = [2,1,5,6,2,3].The largest rectangle is shown in the shaded area, which has area = 10 unit.

using this logic we can solve max-rectangle(dynamicprogramming)
the link is https://codemummy.blogspot.com/2020/08/Max-rectangle-dynamic-programming.html

lets use stack to solve this problem:
c++implementation:
t is the no of test cases:
we have used long long instead of int incase if the histogram length is to big:

#include<bits/stdc++.h>
using namespace std;

long long maxareahist(int a[],int n)
{
 long long area=0; int i=0; long long mxarea=0;
 stack<int>s;
 
while(i<n)
{
   if(s.empty() || a[s.top()] <=a[i])
     s.push(i++);
   
   else
   {
       int y= s.top();
       s.pop();
       
       if(s.empty())
       area=a[y]*i;
       else
       area=a[y]*(i-s.top()-1);
       
       mxarea=max(area,mxarea);
   }
}

while(!s.empty())
{   
       int y= s.top();
       s.pop();
       
       if(s.empty())
       area=a[y]*i;
       else
       area=a[y]*(i-s.top()-1);
       
       mxarea=max(area,mxarea);
    
}
   return mxarea; 
}

int main() { int t; cin>>t;
while(t--)
{ int n; cin>>n;
int a[n];

for(int i=0;i<n;i++)
cin>>a[i];

cout<<maxareahist(a,n);
cout<<endl;
}
 //code
 return 0;
}